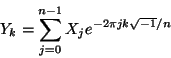 .
.Next: The 1d Real-data DFT, Previous: What FFTW Really Computes, Up: What FFTW Really Computes [Contents][Index]
The forward (FFTW_FORWARD) discrete Fourier transform (DFT) of a
1d complex array X of size n computes an array Y,
where:
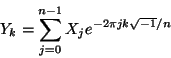 .
.FFTW_BACKWARD) DFT computes:
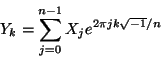 .
.FFTW computes an unnormalized transform, in that there is no coefficient in front of the summation in the DFT. In other words, applying the forward and then the backward transform will multiply the input by n.
From above, an FFTW_FORWARD transform corresponds to a sign of
-1 in the exponent of the DFT. Note also that we use the
standard “in-order” output ordering—the k-th output
corresponds to the frequency k/n (or k/T, where T
is your total sampling period). For those who like to think in terms of
positive and negative frequencies, this means that the positive
frequencies are stored in the first half of the output and the negative
frequencies are stored in backwards order in the second half of the
output. (The frequency -k/n is the same as the frequency
(n-k)/n.)